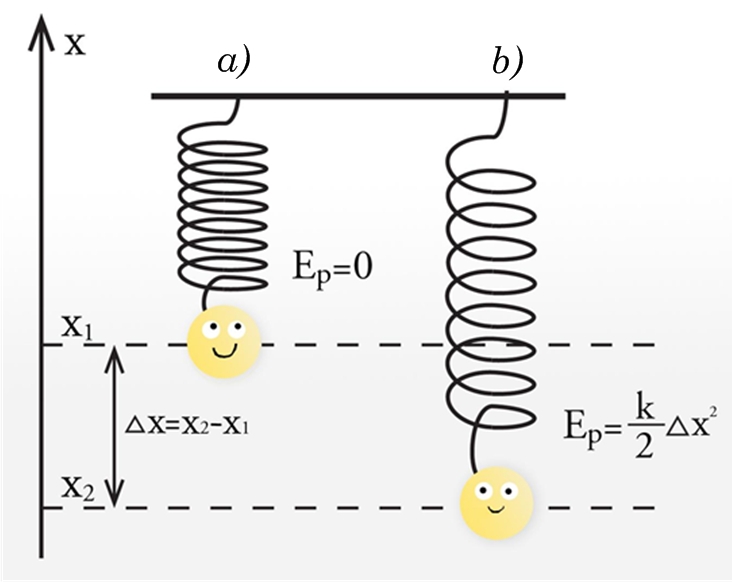
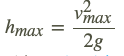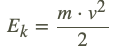Ja ķermeņa kustību neietekmē ārēji apstākļi, piemēram, nepastāv mijiedarbība ar citiem ķermeņiem, nav berzes vai pretestības spēku, tā pilnā mehāniskā enerģija laikā nemainās.

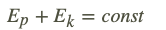
Balstoties uz to, ka kinētiskā enerģija kustības sākumā ir vienāda ar potenciālo enerģiju kustības augšējā punktā, aprēķiniem var tik izmantotas vēl divas formulas.Ja ir zināms maksimālais uzlidošanas augstums, tad var aprēķināt maksimālo kustības ātrumu ar formulu 

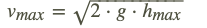
Ja ir zināms maksimālais kustības ātrums, tad var aprēķināt maksimālo uzlidošanas augstumu ar formulu 

Potenciālā enerģija piemīt visiem ķermeņiem, kuriem piemīt potenciāla spēja paveikt darbu.

Potenciālā enerģija piemīt ķermenim, kurš ir pacelts kaut kādā augstumā virs zemes.

Virs zemes pacelts ķermeņa potenciālā enerģija ir tieši proporcionāli atkarīga masas m, brīvas krišanas paātrinājuma g un atrašanās augstuma h. Šos lielumus apvieno formula:Ep=m⋅g⋅h

Potenciālā enerģija piemīt ķermeņiem, kuri ir elastīgi deformēti

Atsperes svārstu veido nekustīgi nostiprināta atspere kurai ir pielikts ķermenis. Sākumā atsperē iekārtais ķermenis atrodas miera stāvoklī. Lai sāktos svārstības, kādam ārējam spēkam iekārtais ķermenis jāpavelk, piemēram, uz leju. Ja izvirzām ķermeni no līdzsvara stāvokļa un palaižam vaļā, tad notiek brīvās svārstības. 
Atsperes svārsta svārstību periods ir atkarīgs no atsvara masas m un atsperes vai auklas stinguma koeficienta k.

Atsperes svārsta perioda mērvienība SI sistēmā ir sekunde (s).

Enerģiju, kas piemīt tikai kustībā esošam ķermenim, sauc par kinētisko enerģiju.

Padarītais darbs ir vienāds ar enerģijas izmaiņu, kas ir patērēta darba veikšanai.

Ja taisnvirziena kustībā uz ķermeni darbojas nemainīgs spēks, kas ir vērsts pārvietojuma virzienā, tad pastrādātais darbs ir vienāds ar šī spēka un veiktā ceļa reizinājumu.

Ja spēks ir vērsts paralēli pārvietošanas virzienam, tad kosinuss no leņķa ir 1. Tādā gadījumā formula kļūst vienkāršāka: A=F⋅l

ja tievā neizstiepjamā diegā iekārtu mazu lodīti izvirza no līdzsvara stāvokļa un palaiž vaļā, tad lodīte sāk periodiski pārvietoties uz vienu un otru pusi. Šādu lodītes kustību sauc par svārstību kustību, bet izveidoto modeli par matemātisko jeb diega svārstu. Šajā gadījumā pieņem, ka diegam nav masas.

Svārsta kustību var uzskatīt par vienkāršu harmonisku kustību. Diega svārsta jeb matemātiskā svārsta svārstību periods ir atkarīgs tikai no svārsta garuma l un brīvās krišanas paātrinājuma g. Jo garāks svārsts, jo lielāks ir svārstību periods.

Ja no kāda augstuma H virs zemes ķermeni izsviež horizontāli ar ātrumu v0, tad ķermeņa kustību varam apskatīt kā divu neatkarīgu kustību rezultātu. Par koordinātu sistēmas sākumpunktu izvēlamies izsviešanas punktu, X asi izsviešanas virzienā un Y asi virzienā lejup.

Par mehāniskām svārstībām sauc tādu kustību, kurā no stabila līdzsvara stāvokļa izvirzīts ķermenis periodiski atgriežas tajā.

Svārstību periods T ir laiks, kādā notiek viena pilna svārstība.

Svārstību periodu aprēķina pēc formulas T=t/n, kur
T – svārstību periods, s
t – svārstību laiks, s
n – svārstību skaits.

Svārstību skaits laika vienībā (sekundē) ir svārstību frekvence ν 

Svārstību frekvenci aprēķina pēc formulas υ=n/t, kur
υ – svārstību frekvence, Hz
t – svārstību laiks, s
n – svārstību skaits

Svārstību frekvences mērvienība SI sistēmā ir herci (Hz).
Svārstību periodu un frekvenci saista sakarība υ=1/T.

Svārstību amplitūda A ir ķermeņa maksimālā novirze no līdzsvara stāvokļa

Svārstības, kas norisinās pēc kosinusa vai sinusa likuma, sauc par harmoniskām svārstībām.

Svārstību sistēmā notiek divu enerģijas veidu – potenciālās (stāvokļa) enerģijas un kinētiskās (kustības) enerģijas savstarpējās pārvērtības.

ja no Zemes virsmas vertikāli augšup izsviež ķermeni, un neievēro gaisa pretestību tad:

• uz ķermeni darbojas tikai smaguma spēks, kurš piešķir  paātrinājumu g
• paātrinājums g vienmēr vērsts virzienā uz Zemes centru
• pārvietojoties augšup, ķermeņa kustība ir vienmērīgi palēnināta, jo paātrinājuma vektors vērsts pretēji ātruma vektoram
• pēc augstākā trajektorijas punkta sasniegšanas, sākas ķermeņa brīvā krišana un ātruma vektora virziens sakrīt ar paātrinājuma vektora virzienu